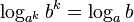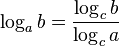Словарь математических терминов

Вы составляете справочник, в котором поясняете термины в различных темах математики, опишите их свойства. Все сведения должны быть точны и корректные. Параметры для записи:размер букв 4(14 pt) ; шрифт Trebuchet ; цветовая гамма 660099. Желаю успеха!

Обзор глоссария по алфавиту

Специальные | А | Б | В | Г | Д | Е | Ё | Ж | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я | Все

Страница: 1 2 3 (Далее)
Все

С

Свойства логарифма

от Смирнова Екатерина - Среда, 13 мая 2009, 14:49

Свойства

Основное логарифмическое тождество:
(замена основания логарифма)

Ключевое(ые) слово(а):

Свойства логарифмов

от Пономаренко Антонина - Вторник, 5 мая 2009, 20:43

Свойства логарифмов:

$\log_a a = 1;\;\log_a 1 = 0$
$\log_a (bc)\ = \log_a b + \log_a c$
$\log_a \frac{b}{c} = \log_a b - \log_a c$
$\log_a (b^p) = p\ \log_a b$
$\log_a \sqrt[c] {b} = \frac{1}{c} \log_a b$
${\log_{a^q}{b}}^p = \frac{p}{q}\log_a{b}$
$\log_{a^k} b^k = \log_a b$
$\log_a b = \frac{\log_c b }{\log_c a}$
$\log_a b = \frac {1}{\log_b a}$
$a^{log_c d}=d^{log_c a}$

Ключевое(ые) слово(а):

Свойства призмы

от Билько Мария - Суббота, 2 мая 2009, 20:41

Свойства призмы:

1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
3. Боковые ребра призмы равны.

свойства тетраэдра

от Смирнова Екатерина - Среда, 13 мая 2009, 14:58

Свойства тетраэдра:

Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину тетраэдра с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.

Ключевое(ые) слово(а):

Сегмент

от Чернявская Кристина - Среда, 6 мая 2009, 19:28

Сегмент - часть круга, ограниченная дугой и стягивающей ее хордой.

Ключевое(ые) слово(а):

Сектор

от Лукьяничева Саша - Среда, 22 апреля 2009, 18:35

Сектор- часть круга, ограниченная 2 радиусами и дугой между ними. Площадь сектора равна 1/2 ar, где r — радиус круга, a — угол между радиусами, ограничивающими сектор, в радианах.

Сектор.

от Лукьяничева Саша - Среда, 22 апреля 2009, 18:36

Сектор- часть круга, ограниченная 2 радиусами и дугой между ними. Площадь сектора равна 1/2 ar, где r — /onmouseclick>радиус круга, a — угол между радиусами, ограничивающими сектор, в радианах.

Секущая

от Айталиева Юлия - Четверг, 7 мая 2009, 14:41

Прямая c, пересекающая прямые a и b называется их секущей. Пусть A и B — различные точки пересечения прямой c с прямыми a и b соответственно, точка P лежит на прямой a, а точка Q на прямой b. Если точки P и Q расположены в разных полуплоскостях относительно прямой c, то углы PAB и QBA называются внутренними накрест лежащими. Если же точки P и Q расположены в одной полуплоскости относительно прямой c, то углы PAB и QBA называются внутренними односторонними.

Ключевое(ые) слово(а):

Симметрия

от Лукьяничева Саша - Суббота, 2 мая 2009, 16:39

Симметрия- в геометрии — свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.

Симметрия относительно прямой

от Пилат Яна - Понедельник, 4 мая 2009, 17:55

Симметрия геометрической фигуры относительно прямой - это такое преобразование фигуры, когда каждая точка одной фигуры находится на таком же расстоянии от прямой, называемой осью симметрии, что и симметричная ей точка второй фигуры. Расстояние измеряется по перпендикуляру к оси симметрии.

Ключевое(ые) слово(а):

Страница: 1 2 3 (Далее)
Все